阅读：0
听报道
墓葬中出现了两只鹦鹉螺酒杯，它们的口沿和背部被装上青铜扣箍，螺壳上被精细地画上类似鸳鸯或鹦鹉的图案。酒杯内部各有30多个彼此隔离的空腔，彼此只有一个小孔相通，倒酒时可以注满每个隔层，饮酒时却不能一饮而尽，让人感觉里面的酒总也喝不完。唐代诗人李白用“鸬鹚杓，鹦鹉杯，百年三万六千日，一日须倾三百杯”这样的诗句，来形容用鹦鹉螺杯喝酒的乐趣.
现代人看到鹦鹉螺的壳,首先是感受到曲线的优美,为什么优美?因为它们是所谓”黄金螺线”
解释黄金分割; 把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。其比值是一个无理数，取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽，因此称为黄金分割
黄金矩形,黄金比例的矩形，即长宽之比为1.618:1，接着在矩形内截出最大的正方形，它应该是以原矩形的宽为边长的，那么剩下的仍是一个黄金比的矩形，它的长宽比为1:0.618，再以它的宽为边长截出一个正方形，得到的仍是一个黄金比矩形……不断重复这一过程，再将所有的正方形的中心以平滑的曲线连接起来，得到的螺旋形曲线叫做“黄金螺线”。鹦鹉螺的外壳形状就是一条黄金螺线。
这就是黄金分割律，由公元前六世纪古希腊数学家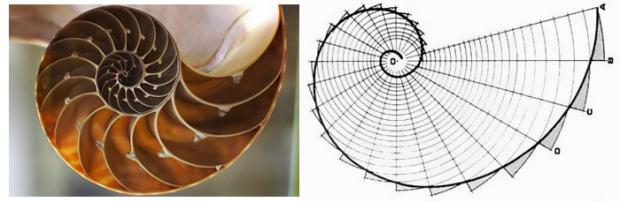
毕达哥拉斯所发现，后来古希腊美学家柏拉图将此称为黄金分割。黄金分割在未发现之前，在客观世界中就存在的，只是当人们揭示了这一奥秘之后，才对它有了明确的认识。当人们根据这个法则再来观察自然界时，就惊奇的发现原来在自然界的许多优美的事物中的能看到它，如植物的叶片、花朵，雪花，五角星……许多动物、昆虫的身体结构中，特别是人体中更是有着丰富的黄金比关系。
毕达哥拉斯所发现，后来古希腊美学家柏拉图将此称为黄金分割。黄金分割在未发现之前，在客观世界中就存在的，只是当人们揭示了这一奥秘之后，才对它有了明确的认识。当人们根据这个法则再来观察自然界时，就惊奇的发现原来在自然界的许多优美的事物中的能看到它，如植物的叶片、花朵，雪花，五角星……许多动物、昆虫的身体结构中，特别是人体中更是有着丰富的黄金比关系。
黄金分割率和黄金矩形能够给画面带来美感，令人愉悦。在很多艺术品以及建筑中都能找到它。埃及的金字塔，希腊雅典的巴特农神庙，印度的泰姬陵，这些伟大杰作都有黄金分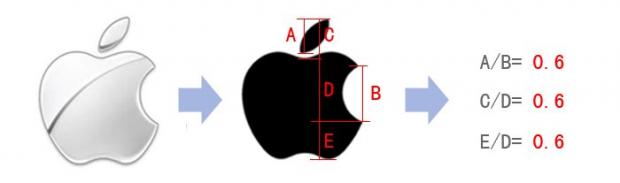
割的影子。
割的影子。
古希腊数学家毕达哥拉斯有句名言“凡是美的东西都具有共同的特征，这就是部分与部分以及部分与整体之间的协调一致。”
看看苹果公司的LOGO,也是黄金分割的应用.
Applelogo
古希腊,罗马人利用黄金分割在数学上总结出斐波那契数列,在建筑,美学等等方面取得了伟大的成就,我们的古人利用黄金螺线的鹦鹉螺在饮酒方面也是很有成就,只是没有上升到数学理论上,不能具体比较.下面拟在数学成就上比较.
古希腊,罗马人在数学上取得许多成就,我们的主流历史学往往会指出我们也有.例如勾股定理,古希腊毕达哥拉斯定理(大约公元前569年，毕达哥拉斯出生于爱奥尼亚的萨摩斯岛)我们会举出战国时期西汉的数学著作 《周髀算经》(公元前100年左右)
《周髀算经》中记录着商高同周公的一段对话。商高说：“…故折矩，勾广三，股修四，经隅五。”商高那段话的意思就是说：当直角三角形的两条直角边分别为3（短边）和4（长边）时，径隅（就是弦）则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。
从年代看,只晚了数百年,但是从技术上看,从《周髀算经》开始,直到近代数学传入中国,我们的算学记载只有3,4,5这三个最基本的勾股数.
西方公元3世纪, 数学家刁潘都完成了勾股数的解析式, 而公元前1800年的一块巴比伦泥版就有(12709,13500,18541)1万多的一组勾股数.差距不是一般的大.
话题：
0
推荐
财新博客版权声明：财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有，未经博主及/或相关权利人单独授权，任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点，不代表财新网的立场和观点。
京公网安备 11010502034662号 